Under major construction.

Re-affirm the atomic nature of matter by tracking the motion of particles undergoing Brownian motion, fitting this data to Einstein's model, and estimating Avogadro's number.

Historical perspective. Reference. The atom plays a central role in 20th century physics and chemistry, but prior to 1908 the reality of atoms and molecules was not universally accepted. In 1827, the botanist Robert Brown observed the random erratic motion of wildflower pollen grains immersed in water using a microscope. This motion would later become known as Brownian motion. Einstein hypothesized that this Brownian motion was the result of millions of tiny water molecules colliding with the larger pollen grain particles. (demo) In one of his "miraculous year" (1905) papers, Einstein formulated a quantitative theory of Brownian motion in an attempt to justify the "existence of atoms of definite finite size." His theory provided experimentalists with a method to count molecules with an ordinary microscope by observing their collective effect on a larger immersed particle. In 1908 Jean Baptiste Perrin used the recently invented ultramicroscope to experimentally validate Einstein's kinetic theory of Brownian motion, thereby providing the first direct evidence supporting the atomic nature of matter. For this work, Perrin won the 1926 Nobel Prize in physics.

The problem. In this assignment, you will redo a version of Perrin's experiment. Your task is greatly simplified because with modern video and computer technology (in conjunction with your programming skills), it is possible to accurately measure and track the motion of an immersed particle undergoing Brownian motion. We supply video microscopy data of polystyrene spheres ("beads") suspended in water, undergoing Brownian motion. Your task is to write a program to analyze this data, determine how much each bead moves between observations, fit this data to Einstein's model, and estimate Avogadro's number.

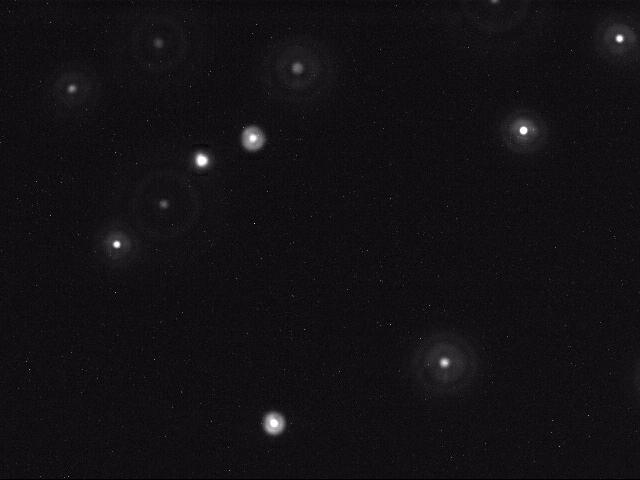
The data.  Each dataset contains a sequence of 640-by-480 gray-scale JPEG images of beads immersed in water. The data was acquired by William Ryu using fluorescent imaging. Here is a movie of several beads undergoing Brownian motion. A typical raw image is shown below.

Each image shows a two-dimensional cross section of a microscope slide at a depth of 50 microns. The beads move in and out of the microscope's field of view. Beads also move in the z-direction, so they can move in and out of the microscope's depth of focus; this results in halos and can also result in beads disappearing from the image. Here are some key parameters.

• Frame rate = 2Hz; Δt = 0.5 seconds per frame.

• Density of water = 1.00g/cm^3.

• Density of beads (latex) = 1.05g/cm^3.

• Diameter of bead = 1 micron. Stddev = 10%.

• Pixels per micron = 5.7.

• Temperature = 75 degrees Fahrenheit.

• F = # JPEG frames = .

Particle identification. The first challenge is to identify the beads amidst the noisy data. Each image 640-by-480 pixels, and each pixel is colored a shade of gray from 0 to 255. Lighter pixels correspond to beads (foreground) and darker particles to water (background). We break the problem into two independent pieces: (i) classifying the pixels as foreground or background, and (ii) finding the disc-shaped clumps of foreground pixels that comprise each bead.

• Foreground / background separation. We use a simple, but effective, technique known as thresholding to separate the pixels into foreground and background components: all pixels with grayscale values below τ are considered foreground, and all others are considered background. For the supplied data, the value τ = 70 results in an effective cut. See resulting picture.

• Blobs. A polystyrene bead is typically represented by a disc-like shape of 20-30 connected foreground pixels. A blob or connected component is a maximal set of connected foreground pixels, regardless of shape or size. For this assignment, we will refer to any blob containing P pixels as a bead. The center-of-mass of a blob (or bead) is the average of the x and y coordinates of its constituent pixels. Create a data type Blob.java that has the following public interface.

  public Blob()                  // construct an empty blob
  public add(int i, int j)       // add a pixel (i, j) to the blob
  public mass()                  // return number of pixels added = its mass
  public distanceTo(Blob b)      // return distance from the center of mass of this blob to b
  public String toString()       // return string representation of this blob's mass and center of mass
  

• Blob detection. To efficiently identify the blobs, we employ a classic algorithm known as depth first search. The key component is a recursive function to identify all foreground pixels connected to some distinguished foreground pixel (i, j). We assume each foreground pixel has an associated boolean value that records whether the particle has already been processed.

  dfs(i, j)

  • If pixel (i, j) is an unvisited foreground pixel, then

    • Add pixel (i, j) to the growing blob.

    • Mark pixel (i, j) as visited.

    • Invoke the dfs function recursively on all neighboring pixels (i+1, j), (i, j+1), (i-1, j) and (i, j-1).

  To determine all blobs (connected components), examine each pixel in raster-scan order (row-by-row, left-to-right), and run depth-first search from the pixel if it is unvisited and corresponds to a foreground pixel. Before running depth-first search, create a new empty blob in which any neighboring foreground pixels will be inserted.

  We want to ignore any particles that touche the boundary of the image frame. The easiest way to do this is to designate all of the pixels in a 1-pixel border as foreground pixels. After doing this, all potential beads that abut the edge of the frame will be marked as visited. We don't want this to count as a bead so we ignore blob 0.

Particle tracking. The second step is to determine how far a bead moved from one time step to the next. We assume the data is such that each bead moves a relatively small amount, and that two beads do not collide. (However, we must account for the possibility that the bead disappears from the frame, either by departing the microscope's field of view in the x or y direction, or moving out of the microscope's depth of focus in the z direction.) Thus, for each bead at time t + Δt, we calculate the closest bead at time t (in Euclidean distance) and identify these two as the same beads. However, if the distance is too large (greater than XYZ) we assume that one of the beads has either just begun or ended its journey. We record the displacement that each bead travels in the Δt units of time.

Data analysis. Einstein theory of Brownian motion connects macroscopic properties (radius, diffusivity) of the beads to microscopic properties (temperature, viscosity) of the fluid in which the beads are immersed. This theory enables us to estimate Avogadro's number with an ordinary microscope by observing the collective effect of millions of water molecules on the beads.

• Estimating the self-diffusion constant. The self-diffusion constant D characterizes the stochastic movement of a molecule (bead) through a homogeneous medium (the water molecules) as a result of random thermal energy. The Einstein-Smoluchowski equation states that the random displacement of a bead in one dimension has a Gaussian distribution with mean zero and variance σ² = 2 D Δt, where Δt is the time interval between position measurements. That is, a molecule's mean displacement in zero and its mean square displacement is proportional to the elapsed time between measurements, with the constant of proportionality 2D. We estimate σ² by computing the variance of all observed bead displacements in the x and y directions. Let (Δx₁, Δy₁), ..., (Δx_n, Δy_n) be the bead displacements, and let r₁, ..., r_n denote the radial displacements. Then
  

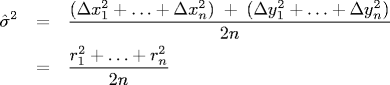
  Since all 2n displacement measurements are statistically independent, σ² has a Chi-square distribution with 2n degrees of freedom. This enables us to compute a 95% confidence interval for σ² as follows:

  

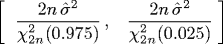
  where χ²_2n(α) is the α-quantile of a Chi-square distribution with 2n degrees of freedom. For example, if n = 100, then the confidence interval is [0.83 σ², 1.23 σ²]. Note that the confidence interval is not symmetric. For our data, Δt = 0.5 so this is a 95% confidence interval for D as well.

     N lower upper
  ----------------
    50 0.772 1.347
   100 0.830 1.230
   150 0.857 1.182
   200 0.875 1.154
   250 0.887 1.137
   500 0.918 1.094
  1000 0.941 1.065
  2500 0.962 1.040
  

• Estimating the Boltzmann constant. The Stokes-Einstein relation asserts that the self-diffusion constant of a spherical particle immersed in a fluid is given by
  

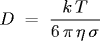
  where T = absolute temperature, η = viscosity of fluid, σ = radius of particle, and k is the Boltzmann constant. The Boltzmann constant is a fundamental physical constant that relates the average kinetic energy of a molecule to its temperature. We estimate k by measuring all of the parameters in the Stokes-Einstein equation, and solving for k. True answer is k = 1.3806503 * 10^-23 J K^-1.

• Estimating Avogadro's number. Avogadro's number N_A is defined to be the number of particles in a mole. By definition, k = R / N_A, where the universal gas constant R is the constant of proportionality in the ideal gas law PV = nRT; it is approximately 8.31457 J K^-1 mol^-1. We use the quantity R / k as our estimate of Avogadro's number. Perrin's experiment yielded one of the earliest estimates of Avogadro's number. True answer = 6.022142 * 10²³.

  reference Diffusion constant might be over-estimated because of hydrodynamic effects (e.g., coupling between particle and the microscope cover slip, coupling between charged particle and its surrounding) reference